로트카-볼테라 방정식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
- 2.1. 모델 개발 배경
- 2.2. 한국 생태학 연구에의 영향
3. 모델의 가정 및 생물학적 해석
4. 시스템 역학
- 4.1. 개체군 평형
- 4.2. 고정점의 안정성
5. 모델의 한계 및 확장
- 5.1. 모델의 한계
- 5.2. 모델의 확장
6. 경제학 및 마케팅 응용
참조

1. 개요

로트카-볼테라 방정식은 포식자와 피식자의 상호작용을 수학적으로 모델링한 것으로, 1910년 알프레드 J. 로트카에 의해 처음 제안되었고, 비토 볼테라에 의해 독립적으로 개발되어 '로트카-볼테라 모델'로 알려졌다. 이 모델은 제1차 세계 대전 중 어획량 변화를 연구하는 과정에서 영감을 받아 개발되었으며, 생태계 내 개체군 변동을 설명하는 데 사용된다. 모델은 포식자와 피식자의 개체수 변화를 나타내는 연립 미분 방정식을 통해 표현되며, 개체군 평형, 안정성 분석, 그리고 모델의 한계와 확장 가능성에 대한 연구가 이루어졌다. 로트카-볼테라 방정식은 경제학 및 마케팅 분야에도 적용되어 경쟁 시장의 역학을 설명하는 데 활용된다.

더 읽어볼만한 페이지

연립 방정식 - 연립방정식
연립방정식은 여러 개의 미지수를 포함하는 방정식들을 묶어 공통된 해를 구하는 데 사용되며, 다양한 분야의 문제 해결에 활용된다.
포식 - 보호색
보호색은 생물이 주변 환경과 유사한 색, 무늬, 형태 등으로 자신을 숨기는 위장 전략으로, 시각적 위장뿐 아니라 후각, 청각적 위장도 포함하며 포식자-피식자 간 공진화에 중요한 역할을 한다.
포식 - 야행성
야행성은 동물들이 포식자 회피, 수분 보존, 자원 경쟁 완화 등의 이점을 얻기 위해 밤에 활동하는 생활 방식이지만, 광공해와 서식지 교란으로 생존에 위협을 받고, 인간의 경제 활동과 건강 문제와도 관련되는 개념이다.
수리생물학 - 계산신경과학
계산신경과학은 컴퓨터 과학과 신경과학의 융합 분야로, 뇌의 정보 처리 과정을 계산 모델로 연구하며, 뇌 기능 설명, 뉴런 및 신경망 모델링, 인공지능 활용 비교 연구, 계산 임상 신경과학 발전 등을 포함한다.
수리생물학 - Folding@home
Folding@home은 단백질 폴딩 연구를 위해 전 세계 컴퓨터 자원을 활용하여 알츠하이머병, 헌팅턴병 등 질병 연구에 기여하는 분산 컴퓨팅 프로젝트이다.

로트카-볼테라 방정식
개요
유형	1차 자율 미분 방정식
분야	수학, 생물학, 화학, 경제학
이름 붙여짐	알프레드 J. 로트카, 비토 볼테라
방정식
일반적인 포식자-피식자 방정식	βxy γy
변수	x: 피식자의 개체 수 y: 포식자의 개체 수
매개변수	α: 피식자의 자연적인 증가율 β: 포식으로 인한 피식자의 감소율 γ: 포식자의 자연적인 감소율 δ: 포식으로 인한 포식자의 증가율
설명
설명	로트카-볼테라 방정식은 포식자와 피식자 사이의 상호 작용을 설명하는 한 쌍의 1차 비선형 미분 방정식이다. 이 방정식은 생태학에서 가장 흔히 사용되어 포식자와 피식자의 개체군 역학을 모델링한다.
역사
개발	이 방정식은 1920년대에 알프레드 J. 로트카와 비토 볼테라가 독립적으로 개발했다. 로트카는 1910년에 자동 촉매 화학 반응 시스템에 대해 같은 방정식을 유도했다.
방정식의 해
해	이 방정식은 해석적으로 풀 수 없지만, 수치적으로 시뮬레이션할 수 있다. 방정식의 해는 포식자와 피식자의 개체수가 시간에 따라 주기적으로 변동하는 것을 보여준다.
안정성
안정성	로트카-볼테라 방정식은 안정적인 평형점을 갖지 않는다. 즉, 포식자와 피식자의 개체수는 영원히 변동한다. 그러나 방정식에 다른 요인을 추가하면 안정적인 평형점을 가질 수 있다.
응용
응용	로트카-볼테라 방정식은 생태학, 경제학, 역학, 화학 등 다양한 분야에서 사용된다. 생태학에서는 포식자와 피식자의 개체군 역학을 모델링하는 데 가장 흔히 사용된다.
기타
참고 문헌	Cooke, D. et al. 1981 Freedman, H. I. 1980 Brauer, F. & Castillo-Chavez, C. 2000 Hoppensteadt, F. 2006

2. 역사

제1차 세계 대전 중 이탈리아 해군과 오스트리아, 헝가리 제국과의 전쟁으로 인하여 아드리아 해역에서의 대규모 어업은 전면 중단되었다. 수년 뒤에 이탈리아의 생태학자 단코나는 어업시장에서 어획량의 통계를 조사한 결과 전쟁 후 상어 등의 육식어의 비율이 전쟁 전보다 매우 높아진 사실을 알게 된 것이다.^[19] 단코나는 전쟁이 상어의 번식에 어떤 영향을 끼치는가에 대해 매우 의아해했다. 활발한 어업으로 물고기 수가 감소하면 포식자인 상어의 개체수도 감소한다. 먹이를 어부에게 빼앗겨 식량부족이 되어 굶어 죽는 상어가 많이 생긴다. 따라서 상어보다 약한 물고기의 수가 훨씬 불어난다. 그러나 전쟁으로 어업이 중단되면 그 반대가 된다. 먹이가 많아지자 상어는 불어나고 그 때문에 약한 물고기는 줄어든다.

비토 볼테라는 단코나가 관찰한 현상을 수학적으로 정리하였다. 오늘날 여러 종류의 물고기가 아드리아 해에서 살지만 단순화하여 분류하면 포식자와 피식자로 나눈다. 포식자와 피식자가 서로 상대의 개체 수에 영향을 미치고 있을 때, 어업 등의 활동으로 양자의 성장률을 저하시키는 요인이 생기면 피식자는 증가하고 포식자는 감소하는 현상이 일어난다.^[19] 볼테라의 법칙은 어떤 살충제에 의한 해충구제의 실패에 의해 실증되었다. 살충제는 바퀴벌레 등 해충만을 죽이는 것이 아니라 그들의 천적인 투구풍뎅이나 새도 죽인다. 해충은 세대 기간이 짧아서 살충제에 곧바로 적응하지만, 포식자는 살충제에 적응할 수 없게 되어 멸종된다. 그래서 해충은 살충제를 뿌리기 전보다 저항력이 커진다. 볼테라의 모델은 후에 미국의 화학자 알프레드 J. 로트카에 의해 로트카-볼테라 방정식으로 정리되고 생태계의 성장이나 물질순환, 화학반응 등 광범위한 생명현상을 수리적으로 분석하는 일에 이용되었다.^[12]^[13]

러시아의 생태학자 가우제, 코스츠킨 그리고 수학자 콜모고르프는 볼테라의 성과를 확장하여 포식자와 피식자 간의 생태학적 경쟁에 대하여 4가지의 경우로 정리하였다.

로트카-볼테라 모델은 1910년 알프레드 J. 로트카에 의해 자동 촉매 화학 반응 이론에서 처음 제안되었다.^[12]^[13] 이는 사실상 로지스틱 방정식이었으며,^[14] 원래 피에르 프랑수아 베르훌스트에 의해 유도되었다.^[15] 1920년 로트카는 안드레이 콜모고로프를 통해 식물 종과 초식 동물 종을 예시로 사용하여 "유기체 시스템"으로 모델을 확장했고,^[16] 1925년에는 자신의 생물수학 서적에서 포식자와 피식자 간의 상호 작용을 분석하기 위해 해당 방정식을 사용했다.^[17] 동일한 방정식 세트는 1926년 수학자이자 물리학자인 비토 볼테라에 의해 발표되었으며, 그는 수리 생물학에 관심을 갖게 되었다.^[13]^[18] 볼테라의 연구는 당시 그의 딸과 교제하고 나중에 사위가 된 해양 생물학자 움베르토 다 안코나와의 상호 작용을 통해 영감을 받았다. 다 안코나는 아드리아해의 어획량을 연구했고, 제1차 세계 대전(1914–18) 동안 포식성 어류의 어획 비율이 증가했다는 것을 알아차렸다. 이는 그를 당황하게 했는데, 전쟁 기간 동안 어업 활동이 매우 줄었고, 피식 어종이 선호되는 어획 대상이었으므로, 직관적으로 피식 어종의 비율이 증가할 것으로 예상했기 때문이다. 볼테라는 다 안코나의 관찰을 설명하기 위해 자신의 모델을 개발했고, 이는 알프레드 로트카와는 별개로 이루어졌다. 그는 그의 출판물에서 로트카의 이전 연구에 대한 공로를 인정했으며, 그 후 모델은 "로트카-볼테라 모델"로 알려지게 되었다.^[20]

이 모델은 나중에 밀도 의존적 피식자 성장을 포함하도록 확장되었고, 기능적 반응의 형태는 C. S. 홀링에 의해 개발되었으며, 이 모델은 로젠츠바이크-맥아더 모델로 알려지게 되었다.^[21] 로트카-볼테라 모델과 로젠츠바이크-맥아더 모델은 모두 포식자와 피식자의 자연 개체군 역학을 설명하는 데 사용되어 왔다.

1980년대 후반, 로트카-볼테라 포식자-피식자 모델(및 일반적인 먹이 의존적 일반화)에 대한 대안으로, 비율 의존적 또는 아르디티-긴즈버그 모델이 등장했다.^[22] 먹이 의존적 또는 비율 의존적 모델의 유효성은 많은 논쟁을 불러일으켰다.^[23]

로트카-볼테라 방정식은 경제학에서 오랫동안 사용되어 왔으며; 그 초기 적용은 일반적으로 1965년^[24] 또는 1967년 리처드 M. 굿윈의 공로로 여겨진다.^[25]^[26]

2. 1. 모델 개발 배경

제1차 세계 대전 중 아드리아 해역에서의 어업 중단은 이탈리아의 생태학자 단코나에게 흥미로운 현상을 관찰할 기회를 제공했다. 전쟁 후 어획량 통계 조사 결과, 전쟁 전보다 상어 등 육식 어종의 비율이 크게 증가한 것이다.^[19] 활발한 어업은 포식자인 상어의 개체 수를 감소시키지만, 어업 중단은 반대로 상어의 번식을 촉진하고 피식자인 물고기의 수를 감소시키는 결과를 낳았다.

비토 볼테라는 단코나가 관찰한 현상을 수학적으로 설명하기 위해 포식자와 피식자 간의 상호 작용을 단순화한 모델을 개발했다.^[19] 이 모델은 어업 활동이 양쪽 어종의 성장률에 영향을 미쳐 피식자는 증가하고 포식자는 감소하는 현상을 설명한다. 볼테라의 모델은 후에 미국의 화학자 알프레드 J. 로트카에 의해 로트카-볼테라 방정식으로 정리되었으며,^[12]^[13] 생태계, 화학 반응 등 다양한 생명 현상을 분석하는 데 활용되었다.

로트카는 1910년 자동 촉매 화학 반응 이론에서 로트카-볼테라 모델을 처음 제안했으며,^[12]^[13] 1920년에는 식물과 초식 동물의 관계,^[16] 1925년에는 포식자와 피식자 간의 상호 작용을 분석하는 데 이 방정식을 사용했다.^[17] 볼테라는 다 안코나의 연구에 영감을 받아 로트카와는 독립적으로 모델을 개발했으며,^[20] 이후 이 모델은 "로트카-볼테라 모델"로 알려지게 되었다.

로트카-볼테라 방정식은 경제학에서도 오랫동안 사용되어 왔으며,^[24] 1960년대 리처드 M. 굿윈에 의해 경제 모델에 적용되었다.^[25]^[26]

2. 2. 한국 생태학 연구에의 영향

로트카-볼테라 모델은 1910년 알프레드 J. 로트카에 의해 처음 제안되었으며,^[12]^[13] 이는 피에르 프랑수아 베르훌스트가 유도한 로지스틱 방정식과 유사했다.^[14]^[15] 1920년대에 로트카와 비토 볼테라는 각각 포식자와 피식자 간의 상호 작용을 설명하기 위해 이 모델을 사용했다.^[16]^[17] 볼테라의 연구는 움베르토 다 안코나의 아드리아해 어획량 연구에서 영감을 받았다.^[13]^[18]^[19]^[20]

이후 C. S. 홀링에 의해 개발된 기능적 반응 형태를 포함하여 로젠츠바이크-맥아더 모델로 확장되었다.^[21] 1980년대 후반에는 아르디티-긴즈버그 모델이 대안으로 제시되었다.^[22] 로트카-볼테라 방정식은 경제학에서도 활용되었는데, 초기에는 리처드 M. 굿윈에 의해 적용되었다.^[24]^[25]^[26]

3. 모델의 가정 및 생물학적 해석

피식자는 포식에 영향을 받지 않는 한 무한정의 식량을 공급받고 기하급수적으로 번식한다고 가정한다. 이러한 지수 성장은 위의 방정식에서 ''αx''라는 항으로 나타난다. 피식자에 대한 포식의 비율은 포식자와 피식자가 만나는 비율에 비례한다고 가정한다. 이는 위의 ''βxy''로 표시된다. ''x'' 또는 ''y''가 0이면 포식은 존재할 수 없다. 이 두 항을 통해 위의 피식자 방정식을 다음과 같이 해석할 수 있다. 피식자 개체수의 변화율은 자체 성장률에서 포식당하는 비율을 뺀 값으로 주어진다.

''δxy''라는 항은 포식자 개체군의 증가를 나타낸다. (포식률과 유사함을 주목하라. 그러나 포식자 개체군이 증가하는 비율이 피식자를 소비하는 비율과 반드시 같지는 않으므로 다른 상수가 사용된다). ''γy''라는 항은 자연사 또는 이주로 인한 포식자의 손실률을 나타낸다. 이는 피식자가 없을 경우 지수 감소를 초래한다. 따라서 이 방정식은 포식자 개체군의 변화율이 피식자를 소비하는 비율에서 고유 사망률을 뺀 값에 따라 달라진다고 표현한다.

로트카-볼테라 포식-피식자 모델은 포식자 및 피식자 개체군의 환경과 생물학에 대한 몇 가지 가정을 한다.

# 피식자 개체군은 항상 충분한 식량을 찾는다.

# 포식자 개체군의 식량 공급은 피식자 개체군의 크기에 전적으로 의존한다.

# 개체수의 변화율은 그 크기에 비례한다.

# 과정 중에 환경은 한 종에 유리하게 변하지 않으며, 유전적 적응은 중요하지 않다.

# 포식자는 무한한 식욕을 가지고 있다.

# 두 개체군 모두 단일 변수로 설명할 수 있다. 이는 개체군이 역학에 기여하는 공간적 또는 연령 분포를 갖지 않는다고 가정하는 것과 같다.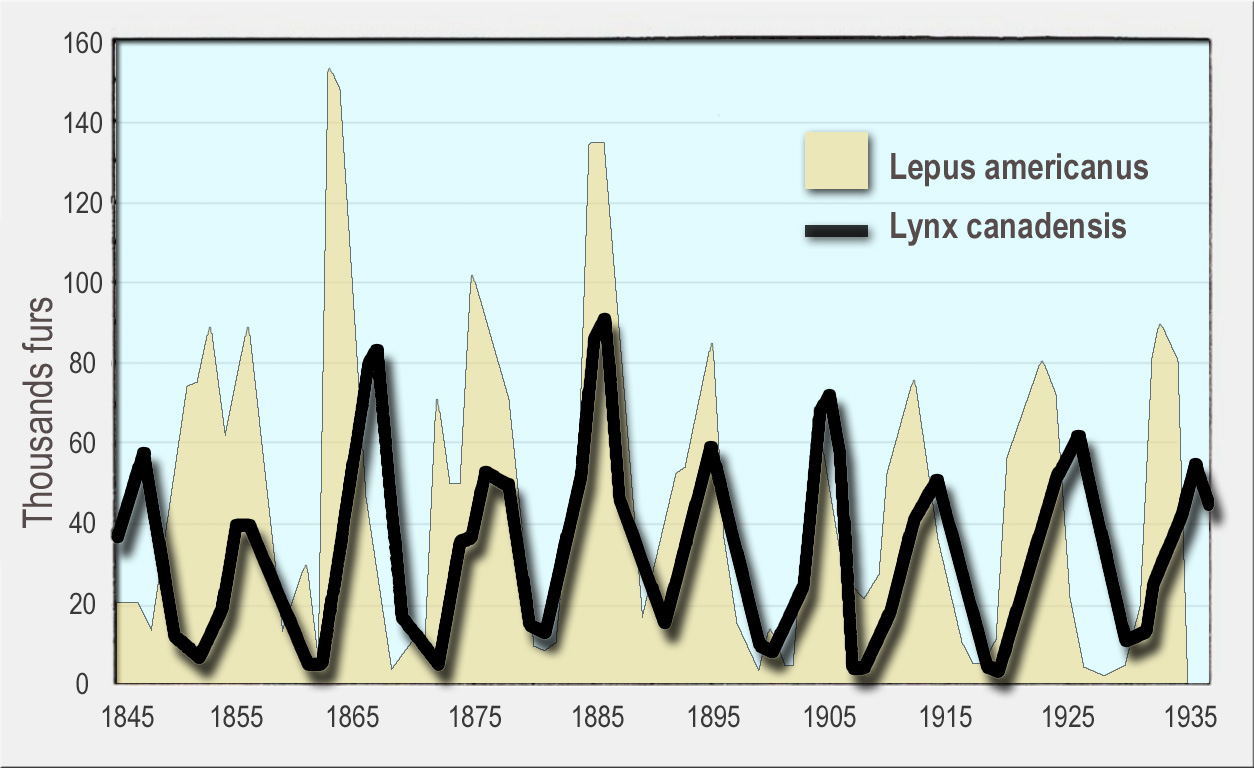

눈신토끼(노란색, 배경)와 캐나다스라소니(검은색 선, 앞쪽) 모피가 허드슨만 회사에 판매된 개체수. 캐나다스라소니는 눈신토끼를 잡아먹는다.

이러한 가정은 자연 개체군에 적용될 가능성이 낮지만, 로트카-볼테라 모델은 포식자와 피식자 개체군의 두 가지 중요한 특성을 보여준다. 첫째, 포식자와 피식자 개체군의 역학은 진동하는 경향이 있다. 허드슨만 회사의 스라소니와 눈신토끼 데이터^[6]와 아일 로열 국립공원의 무스와 늑대 개체군과 같이 자연 개체군에서 포식자와 피식자의 개체수 변동이 관찰되었다.^[7]

둘째, 이 모델의 개체군 평형은 피식자 평형 밀도가 포식자의 매개변수에 의존하고, 포식자 평형 밀도가 피식자의 매개변수에 의존하는 속성을 갖는다. 예를 들어 피식자 성장률 ''α''가 증가하면 피식자 평형 밀도가 증가하지 않고 포식자 평형 밀도가 증가한다. 이는 피식자에게 환경을 더 좋게 만드는 것이 피식자가 아닌 포식자에게 이익이 된다는 것을 의미하며, 살충제 역설 및 비료 효과 역설과 관련이 있다.^[8] 이러한 현상의 예시는 제1차 세계 대전 동안 피식자 성장률이 어획량 감소로 인해 증가하면서 포식성 어류의 어획 비율이 증가한 것이다.

또 다른 예시는 해양의 실험적인 철분 시비에 의해 제공된다. 여러 실험에서 많은 양의 철염이 바다에 용해되었다. 철을 첨가하면 일반적으로 식물 플랑크톤이 짧게 번성하며, 이는 다른 유기체에 의해 빠르게 소비되며, 농축 효과를 주로 포식자 밀도 증가로 제한하며, 이는 차례로 탄소 격리를 제한한다.^[8]

3. 1. 모델의 기본 가정

피식자는 포식에 영향을 받지 않는 한 무한정의 식량을 공급받고 기하급수적으로 번식한다고 가정한다. 이러한 지수 성장은 위의 방정식에서 ''αx''라는 항으로 나타난다. 피식자에 대한 포식의 비율은 포식자와 피식자가 만나는 비율에 비례한다고 가정한다. 이는 위의 ''βxy''로 표시된다. ''x'' 또는 ''y''가 0이면 포식은 존재할 수 없다. 이 두 항을 통해 위의 피식자 방정식을 다음과 같이 해석할 수 있다. 피식자 개체수의 변화율은 자체 성장률에서 포식당하는 비율을 뺀 값으로 주어진다.

''δxy''라는 항은 포식자 개체군의 증가를 나타낸다. (포식률과 유사함을 주목하라. 그러나 포식자 개체군이 증가하는 비율이 피식자를 소비하는 비율과 반드시 같지는 않으므로 다른 상수가 사용된다). ''γy''라는 항은 자연사 또는 이주로 인한 포식자의 손실률을 나타낸다. 이는 피식자가 없을 경우 지수 감소를 초래한다. 따라서 이 방정식은 포식자 개체군의 변화율이 피식자를 소비하는 비율에서 고유 사망률을 뺀 값에 따라 달라진다고 표현한다.

로트카-볼테라 포식-피식자 모델은 포식자 및 피식자 개체군의 환경과 생물학에 대한 몇 가지 가정을 한다.

# 피식자 개체군은 항상 충분한 식량을 찾는다.

# 포식자 개체군의 식량 공급은 피식자 개체군의 크기에 전적으로 의존한다.

# 개체수의 변화율은 그 크기에 비례한다.

# 과정 중에 환경은 한 종에 유리하게 변하지 않으며, 유전적 적응은 중요하지 않다.

# 포식자는 무한한 식욕을 가지고 있다.

# 두 개체군 모두 단일 변수로 설명할 수 있다. 이는 개체군이 역학에 기여하는 공간적 또는 연령 분포를 갖지 않는다고 가정하는 것과 같다.

3. 2. 생물학적 해석

피식자는 포식에 영향을 받지 않는 한 무한정의 식량을 공급받고 기하급수적으로 번식한다고 가정하며, 이는 방정식에서 ''αx'' 항으로 나타난다.^[5] 피식자에 대한 포식 비율은 포식자와 피식자가 만나는 비율에 비례하며, ''βxy''로 표시된다.^[5] ''δxy'' 항은 포식자 개체군의 증가를 나타내고, ''γy'' 항은 자연사 또는 이주로 인한 포식자의 손실률을 나타내며, 이는 피식자가 없을 경우 지수 감소를 초래한다.^[5] 따라서 포식자 개체군의 변화율은 피식자를 소비하는 비율에서 고유 사망률을 뺀 값에 따라 달라진다.^[5]

로트카-볼테라 포식-피식자 모델은 포식자 및 피식자 개체군의 환경과 생물학에 대한 몇 가지 가정을 한다.^[5]

# 피식자 개체군은 항상 충분한 식량을 찾는다.^[5]

# 포식자 개체군의 식량 공급은 피식자 개체군의 크기에 전적으로 의존한다.^[5]

# 개체수의 변화율은 그 크기에 비례한다.^[5]

# 과정 중에 환경은 한 종에 유리하게 변하지 않으며, 유전적 적응은 중요하지 않다.^[5]

# 포식자는 무한한 식욕을 가지고 있다.^[5]

# 두 개체군 모두 단일 변수로 설명할 수 있다. 이는 개체군이 역학에 기여하는 공간적 또는 연령 분포를 갖지 않는다고 가정하는 것과 같다.^[5]

이러한 가정은 자연 개체군에 적용될 가능성이 낮지만, 로트카-볼테라 모델은 포식자와 피식자 개체군의 두 가지 중요한 특성을 보여준다. 첫째, 포식자와 피식자 개체군의 역학은 진동하는 경향이 있다. 허드슨만 회사의 스라소니와 눈신토끼 데이터^[6]와 아일 로열 국립공원의 무스와 늑대 개체군과 같이 자연 개체군에서 포식자와 피식자의 개체수 변동이 관찰되었다.^[7]

둘째, 이 모델의 개체군 평형은 피식자 평형 밀도가 포식자의 매개변수에 의존하고, 포식자 평형 밀도가 피식자의 매개변수에 의존하는 속성을 갖는다. 예를 들어 피식자 성장률 ''α''가 증가하면 피식자 평형 밀도가 증가하지 않고 포식자 평형 밀도가 증가한다. 이는 피식자에게 환경을 더 좋게 만드는 것이 피식자가 아닌 포식자에게 이익이 된다는 것을 의미하며, 살충제 역설 및 비료 효과 역설과 관련이 있다.^[8] 이러한 현상의 예시는 제1차 세계 대전 동안 피식자 성장률이 어획량 감소로 인해 증가하면서 포식성 어류의 어획 비율이 증가한 것이다.

또 다른 예시는 해양의 실험적인 철분 시비에 의해 제공된다. 여러 실험에서 많은 양의 철염이 바다에 용해되었다. 철을 첨가하면 일반적으로 식물 플랑크톤이 짧게 번성하며, 이는 다른 유기체에 의해 빠르게 소비되며, 농축 효과를 주로 포식자 밀도 증가로 제한하며, 이는 차례로 탄소 격리를 제한한다.^[8]

3. 3. 로트카-볼테라 방정식

로트카-볼테라 방정식은 주기적인 해를 가지며, 이는 일반적인 삼각 함수로 간단하게 표현되지 않지만, 다루기 쉽다.^[27]^[28]^[29] 음수가 아닌 매개변수 ''α'', ''β'', ''γ'', ''δ'' 중 어느 것도 0이 아니라면, 세 개는 변수의 정규화에 흡수되어 하나의 매개변수만 남게 된다. 첫 번째 방정식은 ''x''에 대해 동차이고, 두 번째 방정식은 ''y''에 대해 동차이므로, 매개변수 ''β''/''α''와 ''δ''/''γ''는 각각 ''y''와 ''x''의 정규화에 흡수될 수 있으며, ''γ''는 ''t''의 정규화에 흡수될 수 있으므로, ''α''/''γ''만 임의로 남는다. 이는 해의 본질에 영향을 미치는 유일한 매개변수이다.

방정식의 선형화는 포식자 개체수가 순환에서 먹이보다 90° 뒤쳐지는 단순 조화 운동과 유사한 해를 생성한다.^[30]

포식자 개체수의 다양한 초기 조건에 대한 포식자-피식자 문제의 위상 공간 플롯.

토끼(피식자)와 여우(포식자)의 두 종의 동물이 있다고 가정하고, 초기 밀도가 1제곱킬로미터당 토끼 10마리와 여우 10마리이며, 토끼의 성장률과 사망률이 각각 1.1과 0.4이고 여우의 경우 각각 0.1과 0.4라는 매개변수가 주어지면, 두 종의 시간 경과를 도표로 나타낼 수 있다. 시간 간격은 임의적이다.

시간을 나타내지 않고, 모든 시간에 대해 한 축은 피식자의 수를 나타내고 다른 축은 포식자의 밀도를 나타내는 방식으로, 궤도로 위상 공간에서 해를 매개변수적으로 플롯할 수도 있다. 이는 다음 미분 방정식을 통해 변수 ''x''(포식자)와 ''y''(피식자)를 관련시킨다.

:

\frac{dy}{dx} = - \frac{y}{x} \frac{\delta x - \gamma}{\beta y -\alpha}

이 방정식의 해는 닫힌 곡선이며, 변수 분리를 통해 적분하면 다음과 같은 암묵적인 관계가 생성된다.

:

V = \delta x - \gamma \ln(x) + \beta y - \alpha \ln(y),

여기서 ''V''는 초기 조건에 따라 달라지고 각 곡선에서 보존되는 상수 값이다. 시간에 따라

V(x,y)

의 양이 보존되므로, 이 양은 시스템의 해밀턴 함수 역할을 한다.^[33]

모델 연립 방정식에서 피식자의 개체수 증가 속도 ''dx''/''dt''는 다음과 같다.

:

\frac{dx}{dt} = a x - b xy

이는 포식자가 없을 때 피식자 개체수 ''x''가 맬서스 모델처럼 지수 함수적으로 증가한다는 가정()과 포식자가 존재하면 피식자 증식 속도가 억제된다는 가정을 바탕으로 한다. 포식자 수 ''y''와 피식자 개체수 ''x''에 비례하여 피식자 증식 속도가 감소하는 것은 질량 작용의 법칙에 따른다.^[38]

포식자의 개체수 증가 속도 ''dy''/''dt''는 다음과 같다.

:

\frac{dy}{dt} = cxy - dy

이는 피식자가 없을 때 포식자 개체수 ''y''가 감소하고, 포식자의 증가는 포식에 성공한 횟수, 즉 피식자 수 ''x''와 포식자 수 ''y''에 비례한다는 가정을 바탕으로 한다.

3. 4. 방정식의 해

방정식은 주기적인 해를 가지며, 이는 일반적인 삼각 함수로 간단하게 표현되지 않지만 다루기 쉽다.^[27]^[28]^[29] 음수가 아닌 매개변수 , , , 중 어느 것도 0이 아니라면, 변수 정규화를 통해 하나의 매개변수만 남게 된다. 첫 번째 방정식은 에 대해 동차이고, 두 번째 방정식은 에 대해 동차이므로, 매개변수 ''β''/''α''와 ''δ''/''γ''는 각각 와 의 정규화에 흡수될 수 있으며, 는 의 정규화에 흡수될 수 있어, 만 임의로 남는다. 이는 해의 본질에 영향을 미치는 유일한 매개변수이다.

방정식의 선형화는 포식자 개체수가 순환에서 먹이보다 90° 뒤쳐지는 단순 조화 운동과 유사한 해를 생성한다.^[30]

토끼(피식자)와 여우(포식자)의 두 종의 동물이 있다고 가정하고, 초기 밀도, 성장률, 사망률 등의 매개변수가 주어지면, 두 종의 시간 경과를 도표로 나타낼 수 있다. 궤도로 위상 공간에서 해를 매개변수적으로 플롯할 수도 있는데, 이는 시간을 제거하고 두 미분 방정식을 결합하여 하나의 미분 방정식을 생성하여 얻을 수 있다.

:

\frac{dy}{dx} = - \frac{y}{x} \frac{\delta x - \gamma}{\beta y -\alpha}

이 방정식의 해는 닫힌 곡선이며, 변수 분리를 통해 적분하면 다음과 같은 암묵적인 관계를 얻는다.

:

V = \delta x - \gamma \ln(x) + \beta y - \alpha \ln(y),

여기서 ''V''는 초기 조건에 따라 달라지고 각 곡선에서 보존되는 상수 값이다. 이 그래프는 생물학적 모델로서의 응용에 심각한 잠재적 제한(아토-여우 문제)을 갖는다.^[31]^[32]

V(x,y)

는 시스템의 해밀턴 함수 역할을 하며,^[33] 푸아송 괄호를 통해 해밀턴 방정식을 정의할 수 있다. 변수

x

와

y

는 정준 변수가 아니지만, 변환^[34]

p = \ln (x)

와

q = \ln (y)

를 사용하면 해밀턴 방정식의 정준 형태에 도달할 수 있다.

덜 극단적인 예로, , , 이고, , 가 각각 수천을 나타낸다고 가정하면, 원은 포식자 및 피식자의 초기 조건을 나타낸다. 고정점은 (1, 1/2)에 있다. 두 번째 고정점에서 ''J''를 평가하여 얻은 행렬의 고유값은 순수 허수이고 서로 켤레 복소수이므로, 이 고정점은 국소 근방에서 닫힌 궤도의 중심이거나 매력적인 또는 반발적인 나선일 수 있다. 보존적인 시스템에서는 보존량의 최소값과 최대값에서 존재하는 고정점의 국소 근방에 닫힌 궤도가 있어야 한다. 따라서 고정점 주변의 궤도는 닫혀 있고 타원형이므로 해는 주기적이며, 주파수

\omega = \sqrt{\alpha \gamma}

및 주기

T = 2{\pi}/(\sqrt{\lambda_1 \lambda_2})

를 갖는다.

레벨 곡선은 고정점을 둘러싼 닫힌 궤도이며, 포식자 및 피식자 개체군의 레벨은 감쇠 없이 순환하고 진동한다. 운동 상수 의 값은 고정점 근처의 닫힌 궤도에 대해 찾을 수 있다. 를 증가시키면 닫힌 궤도가 고정점에 더 가까워진다. 상수 의 최대값은 최적화 문제를 해결하여 얻으며, 정상(고정)점

\left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right)

에서 다음 값을 갖는다.

K^* = \left(\frac{\alpha}{\beta e}\right)^\alpha \left(\frac{\gamma}{\delta e}\right)^\gamma,

여기서 는 오일러 수이다.

로트카-볼테라 방정식을 해석적으로 풀어 ''x''와 ''y''의 ''t''에 관한 명시적인 해를 얻는 것은 불가능하다. 하지만, 해의 거동을 분석하여 각 개체수가 어떻게 변화하는지를 알 수 있다. 로트카-볼테라 방정식은 역학계의 보존계에 해당하며, 보존량이라고 불리는 양 ''H''를 갖는다.

:

H=cx + by - d \log x - a \log y

여기서, log는 자연로그이다. 우변의 ''H''는 일정한 값을 갖는 상수이며, 시간 경과에 따라 ''x''와 ''y''가 변화해도 ''H''의 값은 항상 동일하게 유지된다. 평형점 (''d''/''c'', ''a''/''b'')에서 ''H''는 최소값을 가지며, ''H'' − ''H_min''는 이 계에서의 랴푸노프 함수이다.^[40]

해 곡선은 평형점 (''d''/''c'', ''a''/''b'') 을 회전하는 폐곡선이다.

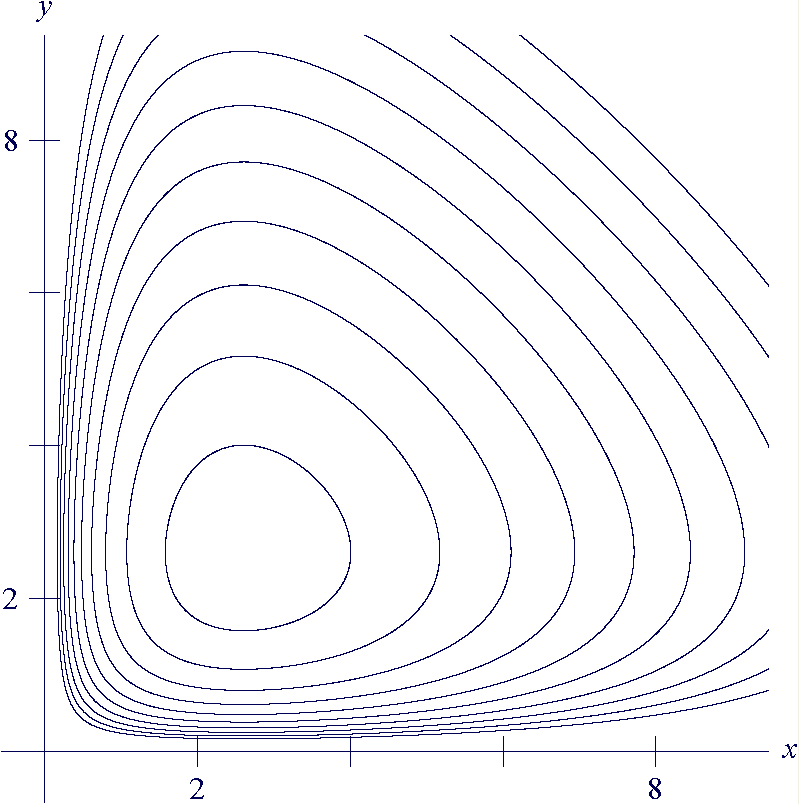
아이소클라인법에 의한 해석만으로는 해 곡선의 형태가 확정되지 않지만, 해 곡선은 평형점 (''d''/''c'', ''a''/''b'') 을 중심으로 반시계 방향으로 회전하는 폐곡선이다. 해 곡선의 형태는 달걀과 같은 모양이며, 피식자 ''x''와 포식자 ''y''의 초기값에 따라 궤도의 크기가 결정된다. ''H''의 각 값에 1개의 폐곡선이 대응하며, ''x''와 ''y''의 1주기 중 평균량은 각각의 평형점 ''d''/''c''와 ''a''/''b''에 일치한다.

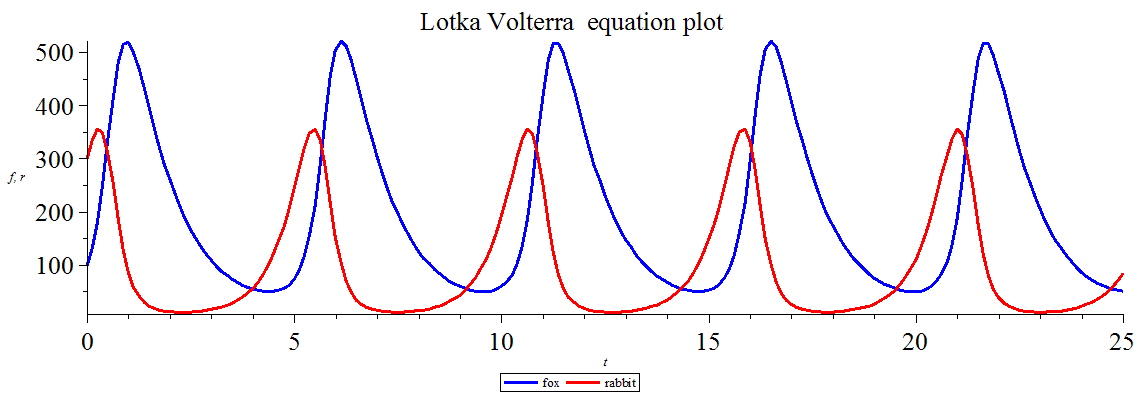
해 곡선이 닫힌 곡선이라는 것은 피식자와 포식자의 개체수가 일정 주기로 진동하고 있다는 것을 의미한다. 개체수의 시간 발전 파형은 복잡한 형태가 되며, 포식자와 피식자의 개체수 변동의 위상은 1/4주기 정도 어긋나 있다.

개체수의 범위를 평형점 근방으로 제한하고 선형 안정 해석에 의해 근사적인 해석을 수행하면, 각 개체수 변동의 진동수를 얻을 수 있다. 이 때의 ''x''와 ''y''는 다음과 같은 관계식으로 나타낸다.

:

C=\frac{a^2c^2}{b^2}x^2  +ad y^2.

여기서, ''C''는 일정값이다. 각 개체수 변동의 진동수 ''ω'' 또는 주기 ''T''는

:

\omega=\sqrt{ad},\quad T=\frac{2\pi}{\sqrt{ad}}

로 주어진다.

4. 시스템 역학

모델 시스템에서, 포식자는 먹이가 풍부할 때 번성하지만, 결국에는 먹이 공급을 초과하여 감소한다. 포식자 개체수가 낮아지면, 먹이 개체수는 다시 증가할 것이다. 이러한 역학 관계는 성장과 감소의 개체수 주기로 지속된다.

로트카-볼테라 방정식을 해석적으로 풀어 ''x''와 ''y''의 ''t''에 관한 명시적인 해를 얻는 것은 불가능하다. 하지만, 다음과 같은 해의 거동을 분석하여 각 개체수가 어떻게 변화하는지를 알 수 있다.

''x''와 ''y''를 변수로 하는 평면(상 평면)상에서, ''dx''/''dt'' = 0 또는 ''dy''/''dt'' = 0을 만족하는 직선에 주목함으로써, 개체수가 어떤 거동을 보이는지 개략적으로 알 수 있다. 이러한 기법을 '''아이소클라인법''' 또는 '''등경사선법'''이라고 부른다.

상 평면에서 가로축을 ''x'', 세로축을 ''y''로 한다. 현실의 생물에서는 개체수는 양의 값이므로, ''x''와 ''y''의 값이 양인 상 평면의 제1사분면이 관심의 대상이 된다. 상 평면상에서는, ''dx''/''dt'' = 0을 만족하는 직선은 ''y'' = ''a''/''b''와 ''x'' = 0의 직선이며, ''dy''/''dt'' = 0을 만족하는 직선은 ''x'' = ''d''/''c''와 ''y'' = 0의 직선이다. 이러한 ''dx''/''dt'' = 0 또는 ''dy''/''dt'' = 0을 만족하는 직선을 '''아이소클라인''' 또는 '''등경사선'''이라고 부른다^[39]. 전자의 직선상에서는 ''dx''/''dt'' = 0이므로, 해 곡선이 이 직선을 지날 때, ''x''의 값은 변하지 않고, ''y''의 값만 변한다. 따라서, 해 곡선은 직선을 상하 방향(''y''축 방향)으로만 통과한다. 그러므로, 이 직선을 '''기울기 무한대의 아이소클라인'''이라고 부른다. 한편, 후자의 직선상에서는 ''dy''/''dt'' = 0이므로, 같은 이유로 해 곡선은 이 직선을 좌우 방향(''x''축 방향)으로만 통과한다. 그러므로, 이 직선을 '''기울기 제로의 아이소클라인'''이라고 부른다.

상 평면에 ''y'' = ''a''/''b''의 수평선과 ''x'' = ''d''/''c''의 연직선을 그리면, 평형점 (''d''/''c'', ''a''/''b'')에서 두 직선은 교차하고, 상 평면은 4개의 영역으로 분류된다. ''y'' = ''a''/''b''의 직선보다 위쪽 영역에서는, ''dx''/''dt''의 값은 항상 음이 된다. 한편, 아래쪽 영역은 ''dx''/''dt''의 값은 항상 양이 된다. 여기서, ''dx''/''dt''의 값이 양이라는 것은 ''x''의 값이 증가하고 있는 상태이며, 음이라는 것은 ''x''의 값이 감소하고 있는 상태이다. 따라서, 방정식의 해의 곡선은, ''y'' = ''a''/''b''의 직선보다 위쪽 영역에서는 왼쪽으로 진행하고, 아래쪽 영역에서는 오른쪽으로 진행할 것으로 예측할 수 있다.

또한 마찬가지로, ''x'' = ''d''/''c''의 직선보다 왼쪽 영역에서는 ''dy''/''dt''의 값은 항상 음이고, 오른쪽 영역은 ''dy''/''dt''의 값은 항상 양이 된다. 이것에 의해 위와 마찬가지로, 방정식의 해의 곡선은, ''x'' = ''d''/''c''의 직선보다 왼쪽 영역에서는 아래쪽으로 진행하고, 오른쪽 영역에서는 위쪽으로 진행할 것으로 예측할 수 있다. 이것들을 조합하면, 해의 곡선은, 평형점 (''d''/''c'', ''a''/''b'')를 중심으로 반시계 방향으로 회전하는 궤도가 된다는 것을 알 수 있다.

4. 1. 개체군 평형

개체수 평형은 두 개체군 수준이 모두 변하지 않을 때, 즉 두 도함수가 모두 0일 때 발생한다.

:

x(\alpha - \beta y) = 0,

:

-y(\gamma - \delta x) = 0.

위 방정식은 두 가지 해를 갖는다.

:

\{y = 0,\ \  x = 0\}

:

\left\{y = \frac{\alpha}{\beta},\ \  x = \frac{\gamma}{\delta} \right\}.

따라서 두 가지 평형점이 존재한다. 첫 번째 해는 두 종 모두 멸종함을 나타내며, 두 번째 해는 두 개체군이 현재의 0이 아닌 숫자를 유지하는 고정점을 나타낸다. 이 평형점에 도달하는 개체수 수준은 매개변수 ''α'', ''β'', ''γ'', ''δ''의 값에 따라 달라진다.

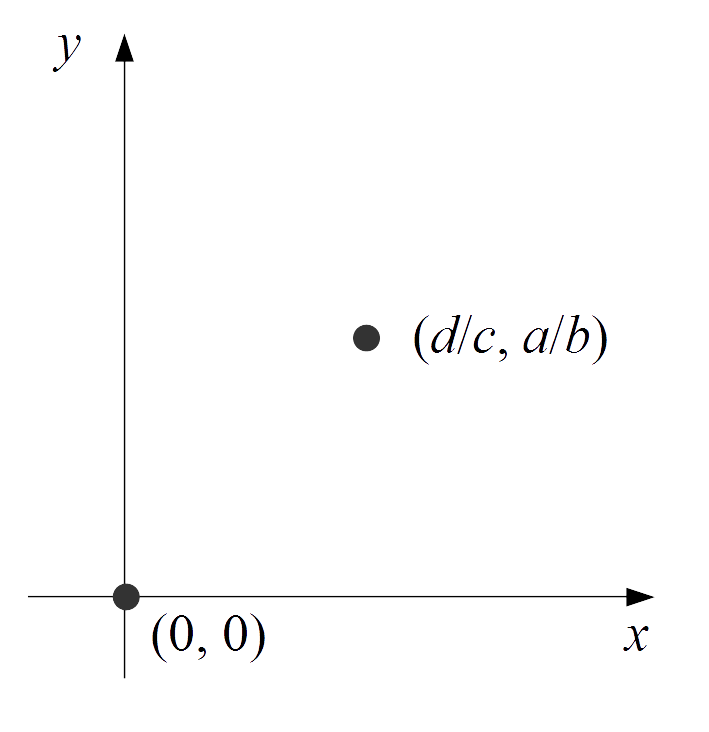
방정식의 ''dx''/''dt''와 ''dy''/''dt''가 모두 0일 때, 개체수 ''x'', ''y''는 시간에 관계없이 변화하지 않는다. 이러한 점을 평형점이라고 한다. 평형점 (0, 0)은 포식자와 피식자 모두 전멸한 상태이고, 평형점 (''d''/''c'', ''a''/''b'')는 포식자와 피식자가 공존하는 상태이다.

평형점 (0, 0) 근방에서 계는 다음과 같이 나타낼 수 있다.

:

\frac{dx}{dt}=ax

:

\frac{dy}{dt}=-dy

행렬 표기를 사용하면,

:

\begin{pmatrix}\frac{dx}{dt} \\\frac{dy}{dt}\end{pmatrix}=\begin{pmatrix}a & 0 \\0 & -d\end{pmatrix}\begin{pmatrix}x \\y\end{pmatrix}

가 된다. ''A''의 고유값은 ''a''와 −''d''로, 양과 음의 고유값을 가지므로 평형점 (0, 0)은 안장점이 된다. 또한, 하나의 고유값은 양수이므로 불안정한 평형점이다.

평형점 (''d''/''c'', ''a''/''b'') 근방에서 계는 다음과 같이 나타낼 수 있다.

:

\begin{pmatrix}\frac{dx}{dt} \\\frac{dy}{dt}\end{pmatrix}=\begin{pmatrix}0 & -\frac{bd}{c} \\\frac{ac}{b} & 0\end{pmatrix}\begin{pmatrix}x \\y\end{pmatrix}

고유값은

\pm i \sqrt{ad}

(

i

는 허수 단위)가 된다. 고유값은 켤레 복소수의 순허수가 되어, 평형점 (''d''/''c'', ''a''/''b'')는 와심점이 된다. 따라서 평형점 근방에서는 상태점이 가까워지지도 멀어지지도 않는 중립적으로 안정한 평형점이 된다.

4. 2. 고정점의 안정성

원점(0, 0)에서의 고정점 안정성은 선형화와 편미분을 사용한 야코비 행렬을 통해 결정할 수 있다. 포식자-피식자 모델의 야코비 행렬은 다음과 같다.

:

J(x, y) = \begin{bmatrix}\alpha - \beta y & -\beta x \\\delta y & \delta x - \gamma\end{bmatrix}.

평형점 (0, 0)에서 야코비 행렬은 다음과 같다.

:

J(0, 0) = \begin{bmatrix}\alpha & 0 \\0 & -\gamma\end{bmatrix}.

이 행렬의 고유값은

\lambda_1 = \alpha

,

\lambda_2 = -\gamma

이다. 모델에서

\alpha

와

\gamma

는 항상 0보다 크므로 고유값의 부호는 항상 다르다. 따라서 원점에서의 고정점은 안장점이 된다. 즉, 불안정하므로 두 종의 멸종은 어렵다.

두 번째 고정점

(\frac{\gamma}{\delta}, \frac{\alpha}{\beta})

에서 ''J''를 평가하면 다음과 같다.

:

J\left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right) = \begin{bmatrix}0 & -\frac{\beta \gamma}{\delta} \\\frac{\alpha \delta}{\beta} & 0\end{bmatrix}.

이 행렬의 고유값은

\lambda_1 = i \sqrt{\alpha \gamma}

,

\lambda_2 = -i \sqrt{\alpha \gamma}

이다. 고유값이 순수 허수이고 서로 켤레 복소수이므로, 이 고정점은 닫힌 궤도의 중심이거나 나선일 수 있다. 보존량

V = \delta x - \gamma \ln(x) + \beta y - \alpha \ln(y)

가 존재하므로, 고정점 주변의 궤도는 닫혀 있고 타원형이며, 해는 주기적으로 진동한다. 이때 주파수는

\omega = \sqrt{\lambda_1 \lambda_2} = \sqrt{\alpha \gamma}

이고, 주기

T = 2{\pi}/(\sqrt{\lambda_1 \lambda_2})

를 갖는다.

레벨 곡선은 고정점을 둘러싼 닫힌 궤도이며, 포식자 및 피식자 개체군의 레벨은 감쇠 없이 순환하고 진동한다. 운동 상수 (또는 ,

K = y^\alpha e^{-\beta y} x^\gamma e^{-\delta x}

)는 고정점 근처의 닫힌 궤도에 대해 찾을 수 있다. 를 증가시키면 닫힌 궤도가 고정점에 더 가까워진다. ''K''의 최대값은 정상(고정)점

\left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right)

에서

K^* = \left(\frac{\alpha}{\beta e}\right)^\alpha \left(\frac{\gamma}{\delta e}\right)^\gamma

값을 가지며, 여기서 는 오일러 수이다.

개체수 ''x'', ''y''가 변화하지 않는 평형점은 다음 두 가지이다.

(x=0,\quad y=0)
$\left(x=\frac{d}{c},\quad y=\frac{a}{b}\right)$

평형점 (0, 0)은 포식자와 피식자가 모두 멸종한 상태이고, 평형점 (''d''/''c'', ''a''/''b'')에서는 포식자와 피식자가 공존하는 상태이다. 평형점 (0,0)은 안장점이며 불안정하다. 평형점 (''d''/''c'', ''a''/''b'')는 켤레 복소수의 순허수인 고유값을 가지는 와심점으로, 중립적으로 안정된 평형점이다.

점 (''d''/''c'', ''a''/''b'')는 중립적인 안정 평형점으로, 궤도는 초기값에 의해 결정되는 닫힌 곡선을 유지한다. 피식자와 포식자는 멸종하지 않고, 개체수가 무한히 증가하지도 않는다. 이는 외부 교란에 대해 원래 궤도로 돌아오지 않는 구조적으로 불안정한 성질을 가진다.

5. 모델의 한계 및 확장

로트카-볼테라 방정식은 현실에 존재하는 많은 계를 고려할 때,

: $\begin{align}\frac{dx}{dt} &= a x - b xy,\\\frac{dy}{dt} &= c xy - d y\\\end{align}$

와 같이 너무 단순한 부분이 있다. 따라서 로트카-볼테라 방정식을 기초로 하여 다양한 모델 연구가 이루어져 왔다。

문제점으로 먼저 지적되는 것은, 포식자가 없을 때 피식자의 증식 속도가 ''ax''가 되어, 무한정 증가한다는 점이다. 실제 계에서는 로지스틱 방정식과 같이 어느 정도 이상 증가하면 자원 부족 등이 발생하여 증식 속도에 제동이 걸린다고 생각하는 것이 합리적이다。 이를 고려하여, 예를 들어, 제1식의 우변 제1항 ''ax''를 로지스틱형 ''ax''(1 − ''x''/''K'')로 대체한 모델을 생각할 수 있다. 여기서 ''K''는 양의 상수이며, 로지스틱 모델에서의 환경 수용력이다。

또한, 피식자 수에 비례하여 무제한으로 포식자 증식 속도가 증가하는 점도 부자연스럽다. 이것도 어느 정도 이상에서 포화된다고 생각할 수 있다。 따라서, 제1식의 우변 제2항 −''bxy''를 −''bxy''/(1 + ''hx'') 등으로 변형하는 것을 생각할 수 있다. 여기서 ''h''는 양의 상수이며, ''x''가 증가해도 이 항에 의한 포식자 1개체당 증식 속도는 ''b''/''h''로 포화된다。

5. 1. 모델의 한계

로트카-볼테라 방정식은 현실에 존재하는 많은 계를 고려할 때 지나치게 단순하다는 한계가 있다. 따라서 이 방정식을 기초로 다양한 모델 연구가 진행되어 왔다.

먼저, 포식자가 없을 때 피식자의 증식 속도가 무한정 증가하는 점이 문제로 지적된다. 실제 계에서는 로지스틱 방정식과 같이 자원 부족 등의 이유로 증식 속도에 제동이 걸리는 것이 일반적이다. 이를 반영하여, 피식자 증식 속도를 로지스틱형으로 대체한 모델을 고려할 수 있다. 이 때, 로지스틱 모델에서의 환경 수용력을 나타내는 양의 상수 ''K''가 사용된다.

또한, 피식자 수에 비례하여 포식자 증식 속도가 무제한으로 증가하는 것도 부자연스럽다. 실제로는 포식자 증식 속도도 일정 수준 이상에서 포화되는 경향을 보인다. 이를 반영하여 포식자 증식 속도 항을 변형한 모델을 고려할 수 있으며, 이 때 ''x''가 증가해도 포식자 1개체당 증식 속도가 ''b''/''h''로 포화되도록 하는 양의 상수 ''h''가 사용된다.

5. 2. 모델의 확장

로트카-볼테라 방정식은 현실에 존재하는 많은 계를 고려할 때,

:

\begin{align}\frac{dx}{dt} &= a x - b xy,\\\frac{dy}{dt} &= c xy - d y\\\end{align}

와 같이 너무 단순한 부분이 있다. 따라서 로트카-볼테라 방정식을 기초로 하여 다양한 모델 연구가 이루어져 왔다.

문제점으로 먼저 지적되는 것은, 포식자가 없을 때 피식자의 증식 속도가 ''ax''가 되어, 무한정 증가한다는 점이다. 실제 계에서는 로지스틱 방정식과 같이 어느 정도 이상 증가하면 자원 부족 등이 발생하여 증식 속도에 제동이 걸린다고 생각하는 것이 합리적이다. 이를 고려하여, 예를 들어, 제1식의 우변 제1항 ''ax''를 로지스틱형 ''ax''(1 − ''x''/''K'')로 대체한 모델을 생각할 수 있다. 여기서 ''K''는 양의 상수이며, 로지스틱 모델에서의 환경 수용력이다.

또한, 피식자 수에 비례하여 무제한으로 포식자 증식 속도가 증가하는 점도 부자연스럽다. 이것도 어느 정도 이상에서 포화된다고 생각할 수 있다. 따라서, 제1식의 우변 제2항 −''bxy''를 −''bxy''/(1 + ''hx'') 등으로 변형하는 것을 생각할 수 있다. 여기서 ''h''는 양의 상수이며, ''x''가 증가해도 이 항에 의한 포식자 1개체당 증식 속도는 ''b''/''h''로 포화된다.

6. 경제학 및 마케팅 응용

로트카-볼테라 모델은 경제학^[9] 및 마케팅^[10]^[11]과 같은 분야에도 적용될 수 있다. 여러 경쟁업체, 상호 보완적인 플랫폼과 제품, 공유 경제 등이 존재하는 시장의 역학 관계를 설명하는 데 사용될 수 있다. 한 경쟁업체가 다른 경쟁업체를 시장에서 몰아내는 상황과 각 회사가 시장 점유율을 안정화하는 균형에 도달하는 상황이 있다. 또한 업계의 주기적인 변화가 있거나, 균형이 없고 변화가 빈번하며 예측 불가능한 혼돈스러운 상황을 설명하는 것도 가능하다.

참조

_[1] 서적 The Mathematical Theory of the Dynamics of Biological Populations Academic Press
_[2] 서적 Deterministic Mathematical Models in Population Ecology Marcel Dekker
_[3] 서적 Mathematical Models in Population Biology and Epidemiology Springer-Verlag
_[4] 간행물 Predator-prey model
_[5] 웹사이트 PREDATOR-PREY DYNAMICS http://www.tiem.utk.[...] 2018-01-09
_[6] 간행물 Do hares eat lynx?
_[7] 간행물 The wolves of Isle Royale display scale-invariant satiation and density dependent predation on moose
_[8] 간행물 Effect of Ocean Iron Fertilization on the Phytoplankton Biological Carbon Pump. 2015-06-03
_[9] 서적 Some quantitative methods and models in economic theory Nova Publishers 2016
_[10] 간행물 A Modified Lotka–Volterra Model for Diffusion and Substitution of Multigeneration DRAM Processing Technologies 2017
_[11] 서적 Forecasting the Dynamics of Market and Technology Ariel University Press
_[12] 간행물 Contribution to the Theory of Periodic Reaction https://zenodo.org/r[...]
_[13] 서적 On the Volterra and Other Nonlinear Models of Interacting Populations Academic Press
_[14] 간행물 The Origins and Evolution of Predator-Prey Theory http://entomology.ws[...]
_[15] 간행물 Notice sur la loi que la population poursuit dans son accroissement https://books.google[...]
_[16] 간행물 Analytical Note on Certain Rhythmic Relations in Organic Systems
_[17] 서적 Elements of Physical Biology Williams and Wilkins
_[18] 간행물 Variazioni e fluttuazioni del numero d'individui in specie animali conviventi
_[19] 서적 Animal Ecology McGraw–Hill
_[20] 서적 Modeling Nature: Episodes in the History of Population Ecology University of Chicago Press
_[21] 간행물 Graphical representation and stability conditions of predator-prey interactions
_[22] 간행물 Coupling in predator-prey dynamics: ratio dependence http://life.bio.suny[...] 2013-06-26
_[23] 간행물 The nature of predation: prey dependent, ratio dependent or neither?
_[24] 간행물 Giuseppe Palomba and the Lotka–Volterra equations
_[25] 서적 Socialism, Capitalism and Economic Growth Cambridge University Press
_[26] 간행물 Richard Goodwin: A Short Appreciation http://www.paulormer[...] 2010-03-22
_[27] 간행물 Parametrische Lösungen der Räuber-Beute-Gleichungen im Vergleich http://archive-ouver[...]
_[28] 간행물 A new transformation for the Lotka-Volterra problem
_[29] 간행물 Limit cycle oscillations, response time, and the time-dependent solution to the Lotka-Volterra predator-prey model
_[30] 서적 Threshold Models in Non-linear Time Series Analysis Springer–Verlag
_[31] 간행물 Migrations in the Rosenzweig-MacArthur model and the "atto-fox" problem http://arima.inria.f[...] 2015
_[32] 간행물 Dependence of epidemic and population velocities on basic parameters http://www.ma.hw.ac.[...]
_[33] 간행물 Hamiltonian structure of the Lotka-Volterra equations https://www.scienced[...]
_[34] 웹사이트 Lotka-Volterra Dynamics - An introduction http://www.ltcc.ac.u[...] 2010-03-02
_[35] 서적 ストロガッツ　非線形ダイナミクスとカオス―数学的基礎から物理・生物・化学・工学への応用まで丸善出版
_[36] 논문 Contribution to the Theory of Periodic Reaction
_[37] 서적 On the Volterra and Other Non-Linear Models of Interacting Populations Academic Press Inc.
_[38] 서적 「数」の数理生物学共立出版
_[39] 서적 生命・生物科学の数理岩波書店
_[40] 학술지 THE PERIOD OF A LOTKA-VOLTERRA SYSTEM http://journal.tms.o[...] The Mathematical Society of the Republic of China 2016-03-02
_[41] 웹사이트 法則の辞典の解説ロトカ‐ヴォルテラの式【Lotka-Volterra equation】 https://kotobank.jp/[...] 朝倉書店 2016-06-11

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com